Pourquoi les ETF à effet de levier ne sont pas une folie, mais un investissement rationnel et efficient
Les ETF à effet de levier souffrent d’une réputation injuste.
On les associe souvent à la spéculation court terme ou au risque excessif.
Pourtant, lorsqu’on les analyse à travers la théorie du CAPM, ils incarnent au contraire
un investissement long terme, rationnel et potentiellement sur-efficient —
à condition d’en comprendre les mécaniques.
La problématique : le bêta-slippage… et le taux implicite qui le compense
Les ETF à effet de levier ont effectivement un défaut :
leur rééquilibrage quotidien crée un bêta-slippage,
c’est-à-dire une perte de performance liée à la volatilité.
Mais cette perte — quantifiable et bornée —
est souvent compensée (voire sur-compensée) par un coût du crédit implicite extrêmement bas,
bien inférieur à ce qu’un investisseur particulier pourrait obtenir avec un prêt classique.
Le cadre théorique : CAPM et droite du marché (SML)
Le CAPM (Capital Asset Pricing Model) explique la relation entre le risque et le rendement :
E[Ri]=Rf+βi⋅(E[Rm]−Rf)E[R_i] = R_f + \beta_i \cdot (E[R_m] - R_f)E[Ri]=Rf+βi⋅(E[Rm]−Rf)
où :
- E[Ri]E[R_i]E[Ri] : rendement attendu de l’actif,
- RfR_fRf : taux sans risque,
- E[Rm]E[R_m]E[Rm] : rendement attendu du marché,
- βi\beta_iβi : exposition au risque systématique (marché).
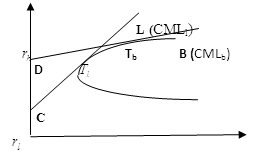
Le CAPM implique qu’il existe une droite unique d’équilibre, la Security Market Line (SML),
sur laquelle tous les portefeuilles efficients se situent.
Pour se déplacer sur cette droite, on ne change pas la composition du portefeuille,
on ajuste le levier :
plus de levier → rendement espéré supérieur,
sans dégradation du ratio de Sharpe.
Ainsi, utiliser du levier n’est pas de la spéculation,
c’est appliquer le CAPM de manière rationnelle :
augmenter le risque pour augmenter proportionnellement le rendement attendu.
Le bêta-slippage : le coût du rééquilibrage quotidien
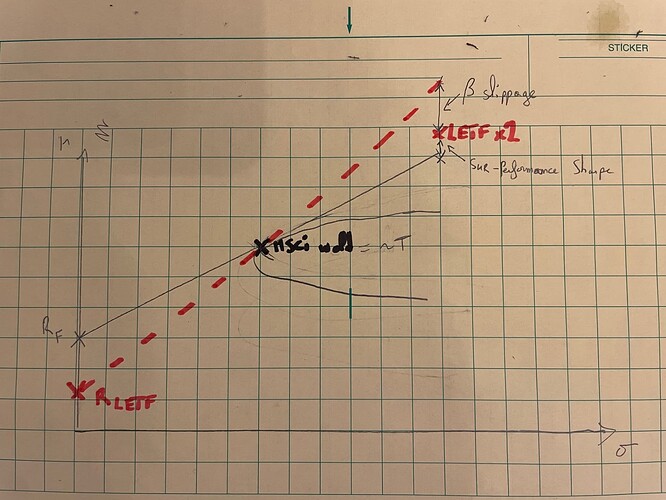
Le bêta-slippage provient de la convexité :
l’ETF à levier x2 réplique la performance quotidienne du sous-jacent,
et la composition des rendements crée une perte mathématique proportionnelle à la volatilité :
Slippage=12L(L−1)σ2\text{Slippage} = \tfrac{1}{2} L (L - 1) \sigma^2Slippage=21L(L−1)σ2
Pour un ETF x2 sur un marché type MSCI World (σ=13%σ = 13 %σ=13%) :
Slippage=0,5×2×1×0,132=1,69%/an\text{Slippage} = 0{,}5 \times 2 \times 1 \times 0{,}13^2 = 1{,}69%/anSlippage=0,5×2×1×0,132=1,69%/an
Ce coût est prévisible, stable, et borne la perte annuelle moyenne due à la volatilité.
Le coût implicite du crédit : bien en dessous du risk-free
Prenons un ETF World classique (frais f1=0,20%f_1 = 0{,}20%f1=0,20%)
et son équivalent x2 (frais f2=0,60%f_2 = 0{,}60%f2=0,60%).
Le taux d’intérêt implicite correspondant au financement du levier est :
rimplicite=f2−f1dette/actif totalr_{\text{implicite}} = \frac{f_2 - f_1}{\text{dette}/\text{actif total}}rimplicite=dette/actif totalf2−f1
Dans un levier x2, la dette = 50 % de l’actif :
rimplicite=(0,60−0,20)/0,5=0,8%/anr_{\text{implicite}} = (0{,}60 - 0{,}20) / 0{,}5 = 0{,}8%/anrimplicite=(0,60−0,20)/0,5=0,8%/an
Autrement dit, le gérant emprunte à 0,8 %,
alors que :
- le taux sans risque est ≈ 3 %,
- un crédit conso coûte ≈ 2–3 %,
- et un levier personnel coûterait bien plus après impôts.
Ce coût implicite est inférieur au risk-free,
ce qui, au sens du CAPM, crée un alpha mécanique positif.
Le coût total du levier devient :
Couˆt total=rimplicite+Slippage=0,8%+1,69%=2,49%\text{Coût total} = r_{\text{implicite}} + \text{Slippage} = 0{,}8% + 1{,}69% = 2{,}49%Couˆt total=rimplicite+Slippage=0,8%+1,69%=2,49%
Et tant que :
Couˆt total<Rf\text{Coût total} < R_fCouˆt total<Rf
le levier reste efficace au sens du ratio de Sharpe.
Conséquence : un levier qui améliore le ratio de Sharpe
Sans levier :
E[Rm]=8%, σ=13%⇒Sharpem=(8−3)/13=0,385E[R_m] = 8%, ; σ = 13% \Rightarrow \text{Sharpe}_m = (8 - 3)/13 = 0{,}385E[Rm]=8%,σ=13%⇒Sharpem=(8−3)/13=0,385
Avec levier x2 :
E[RL]=16−1,69−0,8=13,51%, σL=26%E[R_L] = 16 - 1{,}69 - 0{,}8 = 13{,}51%, ; σ_L = 26%E[RL]=16−1,69−0,8=13,51%,σL=26% SharpeL=(13,51−3)/26=0,405\text{Sharpe}_L = (13{,}51 - 3)/26 = 0{,}405SharpeL=(13,51−3)/26=0,405
Le ratio de Sharpe augmente légèrement → rendement ajusté du risque supérieur,
tant que la volatilité reste modérée (≤ 15 %).
Conclusion : un levier rationnel, pas spéculatif
Les ETF à effet de levier ne sont pas des produits de casino.
Ce sont des outils permettant d’appliquer la théorie financière la plus fondamentale :
le risque doit être rémunéré, et le levier en optimise la rémunération.
Pour un investisseur :
- jeune,
- long terme,
- rationnel,
un ETF x2 représente une solution efficiente pour augmenter son exposition sans dégrader son profil de risque ajusté.
Et c’est là que beaucoup se trompent
La plupart des vulgarisateurs — y compris les Youtubers finance les plus suivis, ou Mounir Laggoune et d’autres créateurs sérieux — déconseillent ces produits au nom d’un risque mal compris.
Ils parlent n’évoque que le beta slippage et son effet négatif et sans le quantifier.
C’est faux, du moins incomplet.
Le bêta-slippage existe, mais il est mathématiquement borné et compensé par un coût d’emprunt implicite bien inférieur au taux sans risque.
Autrement dit, le rendement espéré net reste supérieur, pour un ratio de Sharpe équivalent voire meilleur.
Ce que devraient faire les investisseurs vraiment rationnels
Les investisseurs rationnels — et je crois que beaucoup sur ce forum le sont —
devraient s’intéresser de près à ces ETF à effet de levier,
dans la limite :
- d’une diversification prudente,
- d’un levier modéré (x2 maximum),
- et des contraintes d’éligibilité PEA.
Cela permet de rester sur la droite du marché définie par le CAPM,
mais plus haut : même efficacité, rendement supérieur.
En revanche…
Au-delà de x2 (x3, x4, x5), le bêta-slippage croît quadratiquement :
Slippage∝L(L−1)\text{Slippage} \propto L(L-1)Slippage∝L(L−1)
Il devient alors nettement supérieur au gain de coût implicite,
rendant ces produits inefficaces et purement spéculatifs.
En résumé
- Le CAPM enseigne que le levier n’est pas un excès de risque, mais un ajustement rationnel du rendement.
- Le bêta-slippage existe, mais reste mesurable et compensable.
- Le coût implicite de la dette (≈ 0,8 %) est inférieur au risk-free (≈ 3 %).
- Le ratio de Sharpe est identique, voire légèrement supérieur.
- Et les ETF x2 sont des outils cohérents pour les profils jeunes, long terme, rationnels.
. Le potentiel drawdown doit être mis mis en perspective des capacités de chacun : chacun est libre de (et devrait) fixer le risque maximum qu’il peut encaisser, mais cela n’empeche en rien le fait que l’ETF à effet de levier peut avoir un ratio de sharpe supérieur qu’un meme ETF sans levier
